ホントに久々の更新です。
Twitterでタイトルの件がわからないというのを見かけて、「あれ?うちのWebページに書いてなかったっけ?」とこそっと確認したら、思いっきりすっ飛ばしてた。
てことで、ブログの記事で説明します。
なお、この記事は以下のことを把握していることを前提としています。
(1)重回帰分析による交互作用効果(2要因)の検討の基本を把握していること。
把握していない場合はAiken & West(1991)あるいは私のWebサイト(以下のリンク)を読んでください。
重回帰分析で交互作用効果を検討する方法 -kazutan on web
(2)高校1年程度の数学を理解していること。
また、この内容はAiken & West(1991)のp.23-24に2-wayが、p.58-59に3-wayがちょろっと記載してあります。
今回は2-wayをメインで説明します。
○2要因の交互作用項を含む重回帰モデル
まず、この重回帰モデルを確認します。式は以下の通りとします:
ここで、それぞれの非標準化偏回帰係数は算出されているものとします。
まずはこの式を変形し、右辺をXでまとめます:
この(2)式を中心に使っていきます。
○2直線の交点座標の算出
まず、Z-Aboveの単純回帰直線は、(2)式のZにZ-highを代入したものなので、以下の通りです:
そして、Z-belowの単純回帰直線も同様に、以下の通りとなります:
この2直線の式の交点座標が、今回求めるものとなります。
2直線の交点座標の算出方法ですが・・・要するに、2つの方程式で、Yと(この場合は)Xが同値となる場所です。
つまり、(3)式と(4)式を、YとXの連立方程式と見なし、それぞれ求めればいいのです。そこは省略させてください。
この連立方程式を解くと、以下の様になります:
つまり、交点座標は(1)式で出てきている非標準化偏回帰係数で算出することができます。
○3要因の場合は?
考え方は全く一緒です。
ここでは、Yを目的変数、X、Z、Wを説明変数とし、Xの単純回帰直線を考えるとします。
(1)まず重回帰モデルを確認し、一つの変数(X)でくくる
(2)Z-Above & W-Above, Z-Above & W-below, Z-below & W-Aboe, Z-below & W-belowで4つの方程式を作成
(3)グラフにする2つの直線で連立方程式を作成し、交点座標を算出
3要因になると場合分けが増えますから、交点も増えます。なので、交わる2直線の方程式を選んで求めることになります。
○小道具アップデート
私のWebページの統計関連に、統計小道具として2要因交互作用効果のグラフ化Excelファイルをおいていましたが、この交点を自動的に算出するようにアップデートしました。必要であればご利用ください。
統計小道具 -kazutan on web
以上です。
ご指摘・質問がありましたら、私のTwitterアカウント(kazutan)へメンションやDMでお知らせ下さい。
・・・久々の更新、しかも数式を画像化するというので結構手間取った

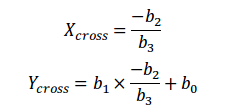
kazutan
ブログ更新| 重回帰分析の交互作用効果における交点座標の求め方 – http://t.co/GUshfbT8
kazutan
というわけで、重回帰分析の交互作用、交点座標について説明するブログ記事を書いた。久々の更新で手間取ってしまった。計算はすごく簡単で、メイン分析で出てきた偏回帰係数でささっと出せます。その理由も難しくないです。 http://t.co/GUshfbT8