相関がある(標準化された)2変量の散布図を回転させるとこうなった

Tweet

[`livedoor` not found]

Check

[`evernote` not found]

散布図を45度回転させると無相関になります。

まあオチは上の通りで、その理屈も図示すればそりゃそうだって感じです。
ただ、「今回扱う2変量は正規分布に従う」と仮定させて下さい。
以下解説しますが、需要としては今回例で使用しているExcelの小技の方かも知れない。

※ 今回関連するExcelの小技を追加しました(2012/12/21)

図による説明

まずは百聞は一見にしかず、Excelで試しに作成したデータでの結果です。

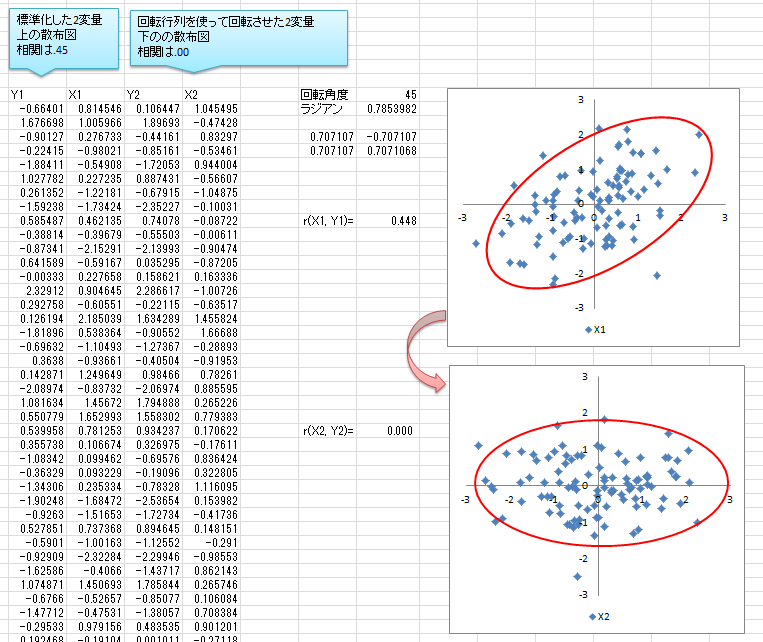
上の散布図がそれぞれ標準化した2変数の散布図で、r=.45です。第一象限と第三象限にプロットが集中し右肩上がりの楕円形となっています。
下の散布図が、2変数を回転行列を用いて原点を中心に45度回転させたものです。四つの象限それぞれにばらけているかと思います。このデータはr=.00です。

無相関になる理由

まず条件を整理します。

• 2変量は標準化されている。従ってM=0, SD=1。
• 原点座標は(0,0)。データの重心も(0,0)。
• この2変量の回帰直線の定数は0,傾きは1(y=x)。
• 「相関がある」→「第一・第三象限」と「第二・第四象限」に差がある。

このことから、標準化された2変数に相関があるならば、その散布図での回帰直線は45度になりますし、楕円もそれに併せて45度傾いた形となります。
では、ここで“原点を中心に座標を回転させる“とどうなるかというと‥‥この楕円が回転することになります。標準化された2変量ですから回帰直線の傾きは45度と決まっているので、45度回転させると縦軸or横軸に重なります。
この状態は、「第一・第三象限」と「第二・第四象限」に差がありません。つまり「相関がない」状態となります。以上です。

補足事項

今回条件として「2変量とも標準化してあること」としましたが、実はしてなくても可能です。わかりやすくするために標準化を条件としました。

2変数が中心化してある場合

「中心化」とはその変数の平均が0となるように変換することです。この場合、回帰直線は原点を通りかつ分布の中心は原点となります。
ただしSDが1で固定されていないため回帰直線の傾きが45度とは限りません。
よって回帰係数から角度を求め、回転行列を作成すれば同じ事ができるでしょう。
なお、中心化であってもSDが同一であれば45度となるはず(たぶん)。

中心化もしていない場合

中心化されていないので重心≠原点なので、ただ回転させても相関は残ります。なので”回転”と”平行移動”を組み合わせます。
回転については上述の通りなので、平行移動について‥‥ですが、手続きは中心化と同じです。てか中心化しろっということになります。

今回使用したExcelの小技について(2012/12/21に追加)

羅列状態になりますが書いていきます。

自分の好きな範囲での乱数の発生

Excelで乱数を発生させる関数は”RAND”ですが、これは”0-1″までの小数となります。自分で好きな範囲で乱数を発生したい場合は以下のように計算すると出せます：
“=[範囲]*RAND()+[最小値]”

なお、小数ではなく整数でほしい場合には、Int関数も組み合わせるとできます:
“=Int([範囲]*RAND())+[最小値]”
※@amano41さんより式のミスを指摘していただきました。ありがとうございます。

ただし、このままだとExcelが再計算する度に値が変化してしまいます。値を変化させたくない場合はコピーして「形式を選択して貼付」→「値のみ」を実行して下さい。

正規分布からランダムに値を取り出す

正規分布に関する関数は色々あるのでわかりにくい上に2010で新たに追加されていたりしますが、今回は2007でも使える方法で説明します。
いわゆる正規分布する変数を作成したいときには、以下の式を入力して必要な数だけフィルを実行してください：
“=NORMINV(RAND(),[分布の平均値],[分布の標準偏差])”

NORMINV関数(引数：[確率][平均][標準偏差]は、[分布の平均値]と[分布の標準偏差]で指定した正規分布上における[確率]に対応する値を返します。
RAND関数は上述の通り”0-1″の乱数を発生させますので、正規分布からランダムな値を持ってくることができます。ただこれだと再計算する度にまた値が変わるのでコピーして値のみの貼付を実行してください。

Excelでの行列演算

Excelで行列の積を計算できます。今回は回転行列を準備して2変数を回転させました。行列の積を算出する関数はMMULT関数です。
ただこの関数でいつも通り計算してもうまくいきません。あらかじめ準備が必要です。
(1)あらかじめ計算結果を出力する先のセルを選択
(2)左上のセルにMMULT関数を挿入して配列に行列の範囲を選択
(3)”Enter(OKボタン)”ではなく、”Ctrl+Shift+Enter”あるいは”Ctrl+Shift押しながらOKボタン”

イメージがつきにくいかもしれませんがこれで計算できます。説明が結構大変なので‥‥「Excel 行列 積」で検索していただけると助かります。

おわりに

ぶっちゃけ「これを知ってて役に立つか?」といわれたら正直うーん‥‥といわざるを得ないほど使えない知識です。
でも、こういうことを考えて理解できるってことは、相関とか標準化とかが整理できているということになるのかなぁと個人的には思います。
ただ若干勢いでやっているところがありますので、「何いってんだ間違ってるぞゴルァ」とかありましたらTwitterアカウントかコメントにお願いいたします。