連続変量とカテゴリカル変数の交互作用を重回帰分析で検討するには

Tweet

[`livedoor` not found]

Check

[`evernote` not found]

タイトルのまんまです。

0.この記事について

私のメインWebサイトには統計関連のコーナーがあり、そこに「重回帰分析で交互作用効果を検討する方法」について解説をしています。
そこにはタイトルの内容についても触れていますが、かつて知人に質問を受けてその返答に送ったメモをupしているだけでした。
しかし結構需要があるようでちょこちょこ問い合わせを受けるようになりましたので、ここで改めて解説をします。

なお、この記事のベースはAiken & West(1991)の”Multipleregression:testing and interpreting interactions”の7章で、そこに自分なりの解釈を加えていますことをご了承ください。

1.前提条件

この記事は以下のことを前提にしています：

• 重回帰分析での交互作用効果の検討について、連続変量のみでの方法を理解している
• 使用しているpredictorはX(連続変量で中心化済み),A(カテゴリカル変数で3水準(a1,a2,a3))
• 2水準の場合は楽なので触れない。4水準以上は3水準の応用なので3水準にだけ触れる

2.カテゴリカル変数の変換

まず、カテゴリカル変数そのままでは重回帰分析を実施できません。何らかの形に変換する必要がありますが、主に2つの方法があります。

2-1.ダミー変数への変換

カテゴリカル変数を「ダミー変数」と呼ばれるものに変更する手法。結果的に(水準数-1)の数だけダミー変数を作ります。具体はこちら：

• A(a1,a2,a3)→D1(0,1,0)
• A(a1,a2,a3)→D2(0,0,1)

これはa1を基準にして(a1-a2)、(a1-a3)という比較を念頭に置いたコーディングです。もし統制群などを設定している場合にはa1を統制群にするとかなりわかりやすいでしょう。
Aという変数の内容をD1とD2という2つの変数に分解、と考えて結構です。D1は「a2が他の条件と違うかどうか」、D2は「a3が他の条件とちがうかどうか」を検出するための変数とイメージするといいかもしれません。
なお、このコーディングではa2とa3の比較はそれほど積極的に検出しません。その対策は後述します。
また(1,0,0)は不要です。解けなくなります。

2-2.Unweighted Effects Coding

要するに非加重コーディング。具体はこちら：

• A(a1,a2,a3)→E1(-1,1,0)
• A(a1,a2,a3)→E2(-1,0,1)

2-3.どっちがいいの?

どっちもどっちです。詳細はAiken & West(1991)のp.127を参照してください。
ただおそらくこの分析を実施しようと思っている方は「連続変量の効果が、カテゴリカル変数の違いによってどう変わってくるか」というカテゴリカル変数によるmoderating effectを検討しようとしている人が多いと思います。
もしそうならダミー変数を使用する方が断トツで楽です。
ここではダミー変数(D1とD2)を使用した分析を解説します。

3.分析モデル

全体的な分析モデル(重回帰式)は以下のようになります：

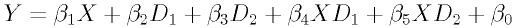
β1-5は各変数の偏回帰係数(標準ではない)、β0は定数項となります。なおβ1の解釈は要注意(後述)。

実際に統計ソフトで分析する際には、以下のステップに従った階層的重回帰分析を実施します：

• Step1:X, D1, D2を投入
• Step2:XD1, XD2を投入

4.主効果の検討について

4-1.主効果を検討する意味

このモデルにおいて主効果を検討するのは「交互作用項がいずれも効果がない場合」でいいのではないかと思います。なぜなら交互作用の効果が認められる状況下では、その主効果は「限定的な効果」をもつわけで、その内容は交互作用によって表現されるからです。
このあたりは研究者のスタンスによって違うと思いますが、私はそう感じます。でなきゃ交互作用項を投入している意味がないし、交互作用項が全て効果がない→主効果の変数だけを投入したモデルと同等かと思うわけで。
以下、交互作用項が有意でないとして、各変数の主効果の見方を説明します。

4-2.連続変量Xの主効果

これは単純で、β1がそのままあてはまります。なのでβ1が有意であれば、(カテゴリカル変数Aの効果を統制した)Xの主効果が有意であるとなります。

4-3.カテゴリカル変数の主効果

ダミー変数D1,D2のいずれかが有意であれば、主効果があると判断します。なお、多重比較については、以下のような状態となります：

1. D1(ns)-D2(ns):a1は他の2つと差がない ※
2. D1(+)-D2(ns):a2 > a1,a3
3. D1(-)-D2(ns):a1,a3 > a2
4. D1(ns)-D2(+):a3 > a1,a2
5. D1(+)-D2(+):a2,a3 > a1 ※
6. D1(-)-D2(+):a3 > a1 > a2
7. D1(ns)-D2(-):a1,a2 > a3
8. D1(+)-D2(-):a2 > a1 > a3
9. D1(-)-D2(-):a1 > a2,a3 ※

上のリストで※印がついている部分は注意が必要で、a2とa3との間に差があるかどうかは(そのままでは)分かりません。それは今回使用したコーディングが「a1を基準としたダミー変数だったから」です。
検討するには追加分析が必要ですが、その手順は以下の通りです：

1. a2を基準としたダミー変数を作成：
• A(a1,a2,a3)→D1_a(1,0,0)
• A(a1,a2,a3)→D2(0,0,1)
2. このD1_aをD1と差し替えて交互作用項を作成→分析を実施
3. D2(←こっちです)の係数がそのままa2とa3の間の検討となります

5.交互作用の検討について

交互作用は、メイン分析のβ4あるいはβ5のいずれかの有意性で判断します。どちらかが有意であれば、交互作用があると判断します。

6.交互作用の下位検定(連続変量の単純傾斜)

先にぶっちゃけますが、メイン分析におけるStep2のβ1はa1条件でのXの単純傾斜です。
これは、「a1条件は(D1=0,D2=0)」であるため、重回帰式に(D1=0,D2=0)を代入したものがa1条件での回帰式になるのですが、

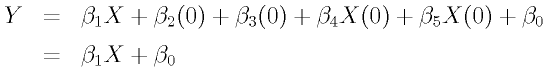
となるためです。もう有意性検定も終わっていますね。

a2条件やa3条件での単純傾斜ですが、ダミーコードを作り直して再度階層的重回帰分析を実施してください。a2を基準としたダミー変数は4.で触れたとおりです。同様にa3を基準としたダミー変数を作成して再度分析してください。

7.交互作用の下位検定(カテゴリカル変数の条件差)

ちょっと面倒ですので段階的に説明します。

7-1.連続変量Xが平均値の場合での、各条件間の比較

a1とa2の比較はD1の係数で、a1とa3の比較はD2の係数で判断してください。Xは中心化されているので、モデル式にX=0を代入するとおのずと導かれます。a2とa3の比較は4-3.で検討しているようにa2を基準としたダミー変数での分析を見て下さい。

7-2.連続変量Xが高い(+1SD)or低い(-1SD)場合での、各条件間の比較

連続変量をもとに、XAboveとXBelowの変数を作成します。連続変量同士での交互作用項を検討する際に使う手法と同一なので省略します。

あとはXをXAbove(Xbelow)に置き換えて分析し、7-1.と同様に分析して下さい。

8.留意事項

箇条書きで簡単に。

• カテゴリカル変数を含んだ交互作用モデルはどうしてもVIFが高くなりますが、(カテゴリカル変数の)中心化がされないためです。この点を割り引いて考えるべきかと。
• 多重比較の検討では、その性質上全体モデルでの平均平方残差を使って検定していますので、ペア間の残差成分というわけではないよ、とAiken & West(1991)でコメントがあります。
• 条件によるXの傾斜の比較については、分析の繰り返しが発生するからボンフェローニ法などで調整することが望まれる、とAiken & West(1991)でコメントがあります。
• 下位検定などにはジョンソン・ネイマン法などもあり、一概に言えません。またGLMでいいじゃんという指摘もあると思います。ただ今回の方法はベースとして知っておいて、さらに「適切だ」と思われる手法に手を伸ばしていくのがいいかなと私は考えています。

9.おわりに

終盤は疲労して一気に書いてしまったのでミスが多くあるかも。てか間違いとかあると思います、すみません。何かありましたら@kazutanもしくはメールなどでご連絡下さい。

あーしかしつかれたわー